Разделение объекта

В предыдущей статье было начато описание преобразования объекта, а так же были заданы некоторые условия по разделению объекта на под области. Сформулируем их ещё раз:

1. Объект должен быть разделён на приблизительно равные области.
2. Граница между областями должна быть минимальна.

Конечно на первых парах я самостоятельно разбивал области. Всё делалось вручную или полуавтоматически. Затем был разработан алгоритм разбиения.

Метод разделения задачи на подзадачи

Так как объект задачи представлен некоторой областью в матрице, то необходимо было разделить эту область на прямоугольники равной площади. Для каждого процесса свой прямоугольник. К тому же желательно было минимизировать количество межпроцессорных взаимодействий.

Для решения этой задачи был предложен следующий алгоритм:

1. Алгоритм начинает выполнение с любой граничной точки, обычно берется левый верхний угол (рис. 1).

2. Затем алгоритм совершает обход границы по часовой стрелке (граница является непрерывной замкнутой линией толщиной в 1 элемент матрицы).

3. Если алгоритм попадает в угол, который направлен внутрь фигуры, то он дочерчивает угол до креста, разделяя таким образом область на три части (рис. 2).

4. После того как все кресты прочерчены мы получаем множество непересекающихся областей прямоугольной формы и различной площади (рис. 3). Для того, чтобы разделить области каждой присваивается свой цвет.

5. Теперь мы проходимся по каждой полученной области и просматриваем соседей (если они есть), если можно объединить текущую область с соседней так, чтобы их общая площадь была ближе к оптимальной площади, то области объединяются.

6. Если площадь области больше оптимальной в какое-либо целое число раз, (или близкое к целому число раз), то область разделяется на это целое число областей.

7. Переходим к следующей области если есть, иначе завершение алгоритма.

Оптимальная площадь вычисляется для данной задачи как общая площадь фигуры, разделенная на количество процессоров. Под близостью к оптимальной площади подразумевается, что остаток от деления площади на оптимальную мал. Насколько мал является параметром алгоритма. Расчёты были произведены с этим параметром равным 30% (т. е. остаток от деления не превышает 30% от оптимальной площади).

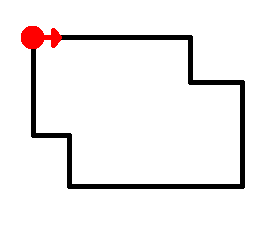
Рис.1. Начало работы алгоритма

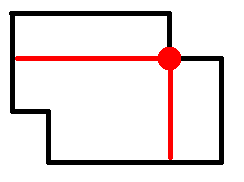
Рис. 2. Деление области в вершине внутреннего угла.

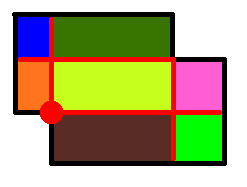
Рис. 3. Деление на области и закраска разным цветом.

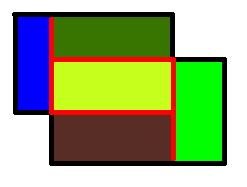
Рис. 4. Пример деления области на 5 процессоров.

Рис. 5. Пример деления на 10 процессоров.

Комментарии по алгоритму

Логическое объяснение этого условия в том, что если результирующий прямоугольник лучше разделится на какое-либо число меньших прямоугольников равных размеров, то имеет смысл объединить две области, а затем разделить общую площадь равномерней. А основная мысль алгоритма заключается в том, что если область делится на примерно равные части, размер которых равен частному общей площади области на количество решателей, то количество таких частей будет примерно равно количеству решателей. 

Так как целью введения данного алгоритма была только автоматизация разделения, поэтому не производится никакой оценки быстродействия и рассмотрения полученных результатов разделения среди всех возможных способов разделения.