Метод с инерцией. Выводы по исследованию

Это завершающая статья по моему курсовому исследованию, так же, здесь я хочу написать о возможных путях, которые по моему мнению могут дать какие-то плоды. Что же после некоторого цикла статей пора сделать выводы по исследованию, которое я проводил в качестве курсовой работы на 4-м курсе. Не кривя душой можно сказать, что ничего особо не получено. Пока не переберёшь все варианты, то нельзя говорить о том, что решения точно нет. Одно можно сказать, так как я делать смысла нет, это не очень эффективно. Пока самые удачные векторы инерций для систем следующие.

Они же на графике

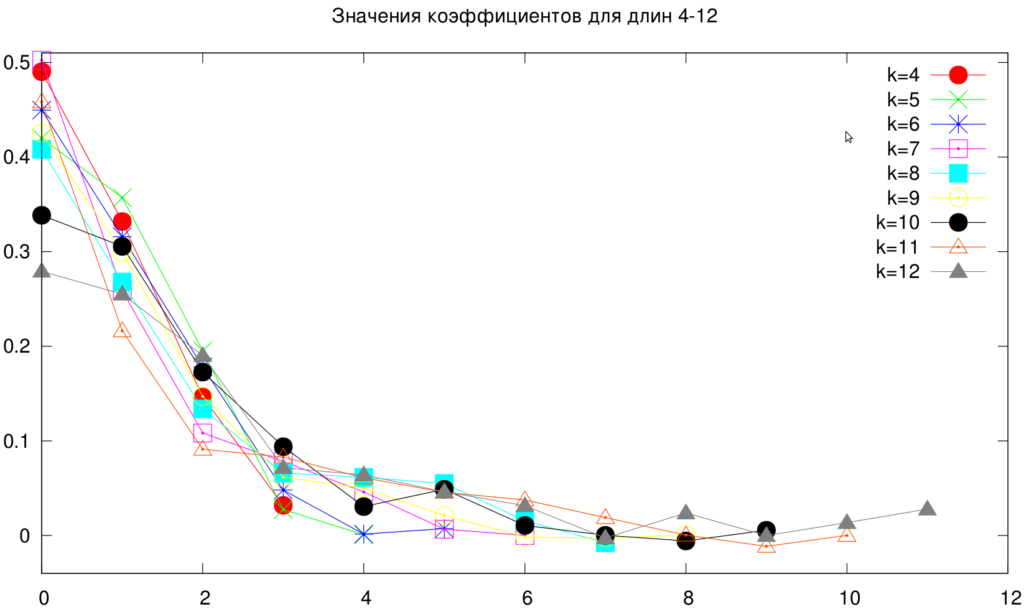
Здесь коэффициенты через запятую. От 4 до 12. Почему я не взял больше? Потому что у меня и не просили брать больше. Да и по графикам видно, что чем больше, тем конечные коэффициенты меньше влияют на решение. Почему-то совсем не выстрелила аппроксимация, думаю можно было бы увеличить степень многочлена и поточнее проверить экспоненту, уж очень она близка к решению.

Замечания

Если матрица и вектор генерируются для каждого элемента так, что их элементы лежат в одном и том же диапазоне чисел — 1-100, то диагональное преобладание делает только хуже: примерно на 4-5% меньше решённых.

Если элементы матрицы и вектора лежат не в одном диапазоне, т. е. элементы матрицы в диапазоне 1-100, а элементы вектора получаются подстановкой в систему случайно сгенерированного вектора, элементы которого так же в диапазоне от 1-100. Соответственно элементы вектора лежат в диапазоне от 1-n*100^p. Где n — размер матрицы, а p — максимальная степень. В таком случае наоборот диагональное преобладание помогает: больше решённых на 25-40%, но при использовании вектора коэффициентов с длинами 1-3 ничего не решается. Целые части решений обычно равны, но после точки нет. Пример:
Настоящее решение:
84.00 90.00 77.00
Полученное решение:
84.2540849328286125152463552 90.3737428074591799597656529 77.0369341204798365336922163

При диагональном анти-преобладании (рецессии), т.е. недиагональные элементы в диапазоне от 1-100, а диагональные элементы равны 1-цам. Если элементы вектора так же в диапазоне 1-100, то вектора 1-3 решают достаточно большое количество систем ~50%.

Дальнейшие планы

1. Сначала стоит разобраться с генерацией систем нелинейных уравнений. Во-первых стоит посмотреть на реальные задачи, чтобы как-то приблизиться к их условиям, а так же просто знать размерность. Может быть мои значения 1-100 никому не нужны, а более важны дробные числа 0-1.
2. Эксперименты стоит проводить для разного типа матриц, но все матрицы для эксперимента должны быть постоянными. Иными словами, если для каждого эксперимента генерировать матрицы случайно, то метод случайного поиска может «заблудиться». Либо выбрать более устойчивый метод и более высокую границу переходу, на которую бы не влиял шум случайных генераций.
3. После попробовать различные размеры вектором, от 2, до размерности матрицы, либо количества элементов матрицы, чтобы понять при какой длине вектора начинают вырождаться (конечные коэффициенты обращаются в 0). Сильно увлекаться не стоит.
4. В конечном счёте аппроксимировать более точными функциями (многочленом большей степени или экспонентой с большим числом членов). Возможно аппроксимация как-то связана со степенью генереруемых систем.
5. Если совсем ничего не будет получаться, то сужать область, может степени только 2 брать или вроде того.