Аппроксимация вектора коэффициентов

Аппроксимация вектора коэффициентов была сделана в математических пакетах. Пока делал работу научился пользоваться gnuplot, для того, чтобы рисовать графики, Octave и SciLab для вычислений. Сейчас уже не скажу точно в каком из этих пакетов было получено данное решение. Точки для графиков тоже стёрлись, поэтому приложу снимки экранов с pdf. Случайным поиском были подобраны коэффициенты инерции, затем я их аппроксимировал.

В качестве функций были выбраны квадратичная и кубическая функции.

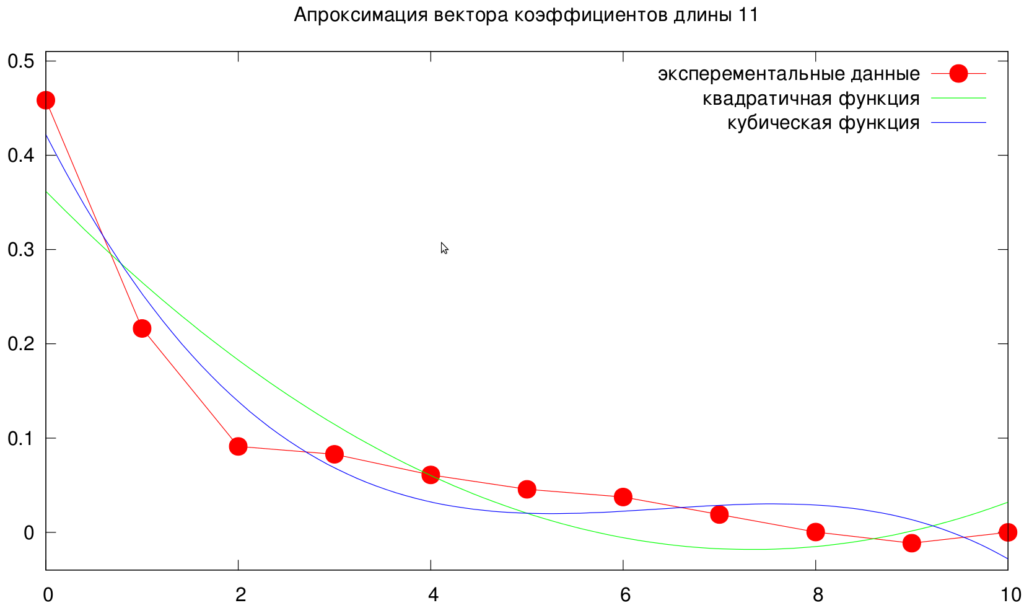
Видно, что кубическая функция лучше (что и не удивительно), но всё ещё есть достаточные перегибы, поэтому была ещё аппроксимация экспоненты.

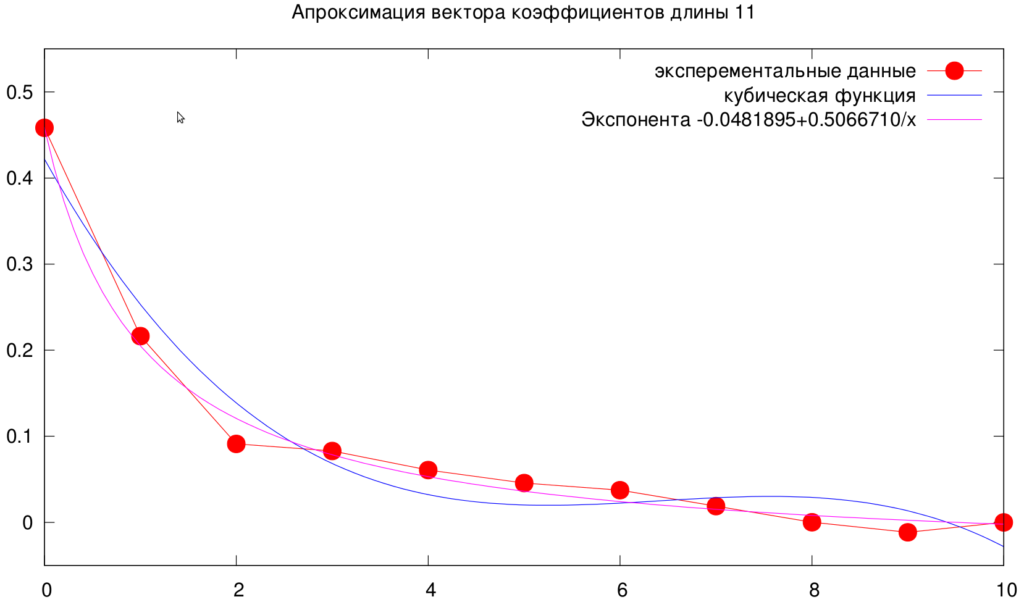
Видно, что экспонента подходит заметно лучше, чем кубическая функция. Однако, это ничего не дало. Если вместо коэффициентов инерции подставлялась значения экспоненты, то толку от этого не было. Решаемость была существенно хуже, либо вообще падала до 0. Честно говоря я был в тупике, поскольку когда учишься в школе или ВУЗе, то это являлось бы конечным решением, а в реальной жизни вышло так, что конечное решение не подходит, оно просто ничего не решает и те векторы, которые были получены эмпирически подходили больше. Сейчас покажу несколько графиков с этими векторами.

Вектора инерции

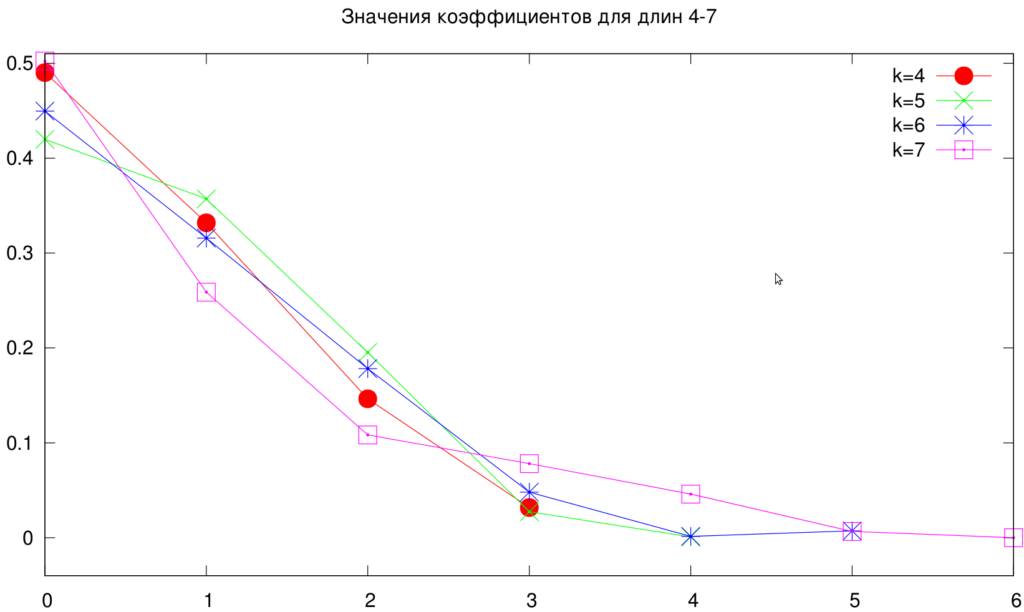
Здесь отображены вектора размера 4-7. После применения случайного поиска. Пока нельзя ни о чём говорить, поэтому переходим к следующему графику.

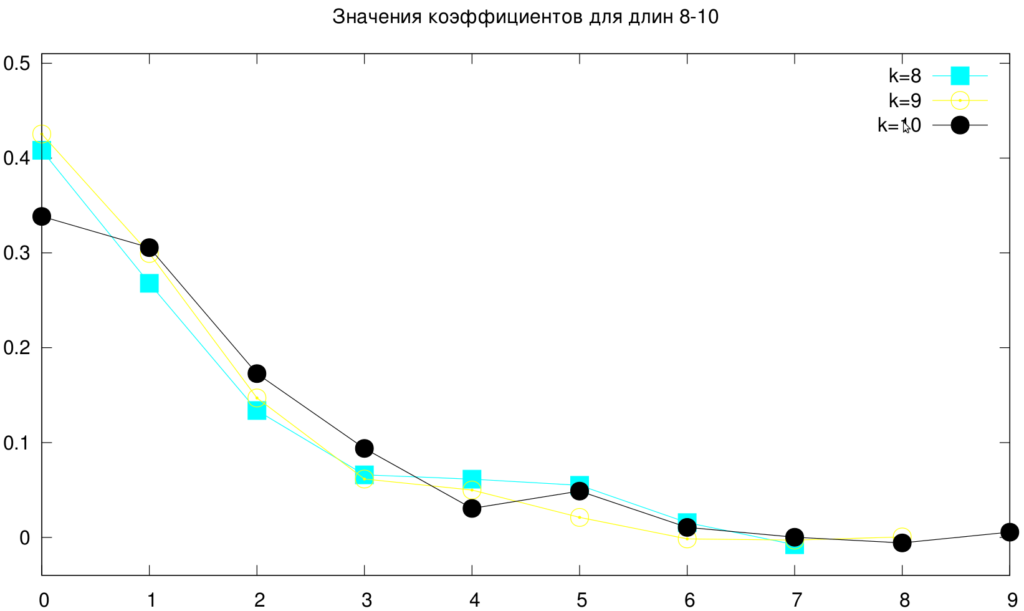
На этом графике отображены вектора размера 8-10. После применения случайного поиска. Видно, что часть точек совпадает, некоторые сильно проваливаются.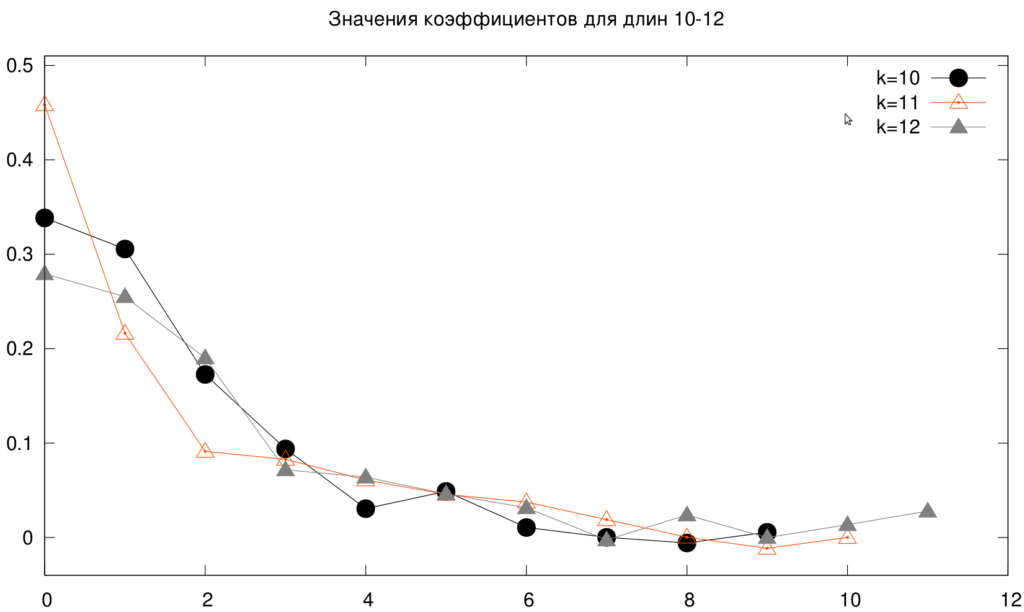

Предпоследний график, здесь вектора 10-12, как и на предыдущих графиках после применения случайного поиска. Наблюдается разнобой как и на предыдущих графиках. Однако, часть точек сливается. Первая точка проваливается по причине того, что сумма коэффициентов должна быть равна 1.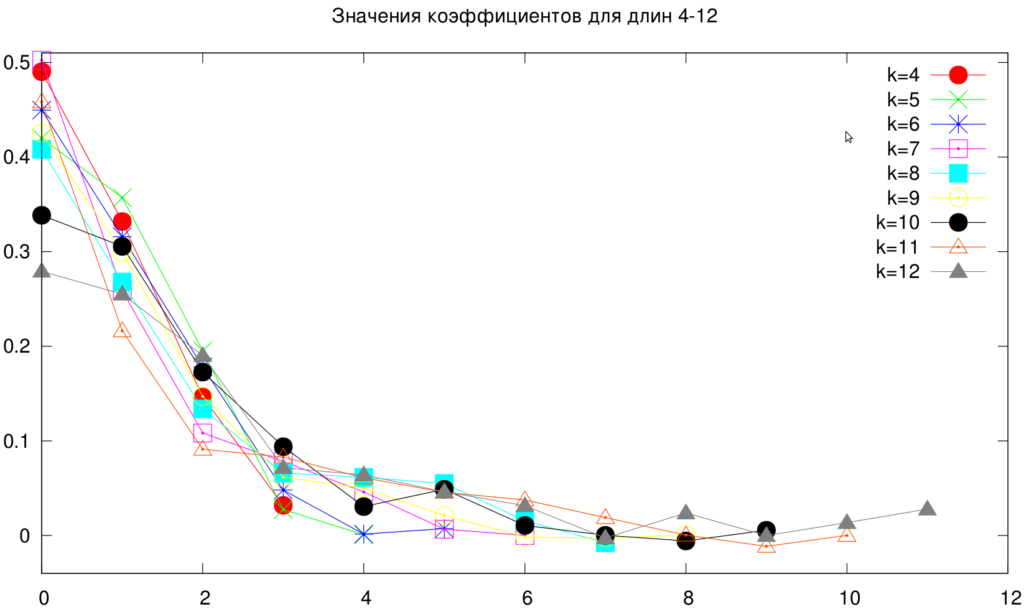

Ну и наконец график сразу со всеми векторами, которые были использованы в экспериментах. Графики перемешиваются, то сливаются, то отдаляются. Думаю это последствия применения алгоритма случайного поиска. Поэтому точки «пляшут». Одно можно сказать точно — заметен резкий провал, а потом плато и даже некоторое увеличение, а это значит, что первые 4-5 коэффициентов самые важные, остальные же вносят меньший вклад. Думаю они нужны для того, чтобы система не зацикливалась. Отсюда следует, что слишком большая инерция не имеет смысла.